RSA Algorithm With Examples

 RSA Algorithm

The RSA algorithm (Rivest-Shamir-Adleman) is the basis of a cryptosystem -- a suite of cryptographic algorithms that are used for specific security services or purposes -- which enables public key encryption and is widely used to secure sensitive data, particularly when it is being sent over an insecure network, such as the internet.

Public key encryption algorithm:

RSA algorithm is an asymmetric cryptography algorithm. Asymmetric actually means that it works on two different keys i.e. Public Key and Private Key. As the name describes that the Public Key is given to everyone and the Private key is kept private.

The Public key is used for encryption, and the Private Key is used for decryption. Decryption cannot be done using a public key. The two keys are linked, but the private key cannot be derived from the public key. The public key is well known, but the private key is secret and it is known only to the user who owns the key. It means that everybody can send a message to the user using user's public key. But only the user can decrypt the message using his private key.

The Public key algorithm operates in the following manner:

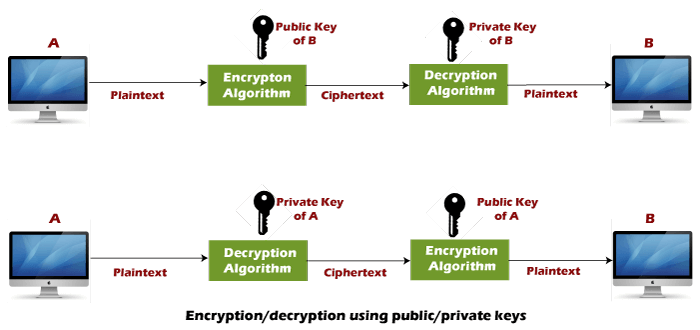
• The data to be sent is encrypted by sender A using the public key of the intended receiver
• B decrypts the received ciphertext using its private key, which is known only to B. B replies to A encrypting its message using A's public key.
• A decrypts the received ciphertext using its private key, which is known only to him.

RSA encryption algorithm:

RSA is the most common public-key algorithm, named after its inventors Rivest, Shamir, and Adelman (RSA).

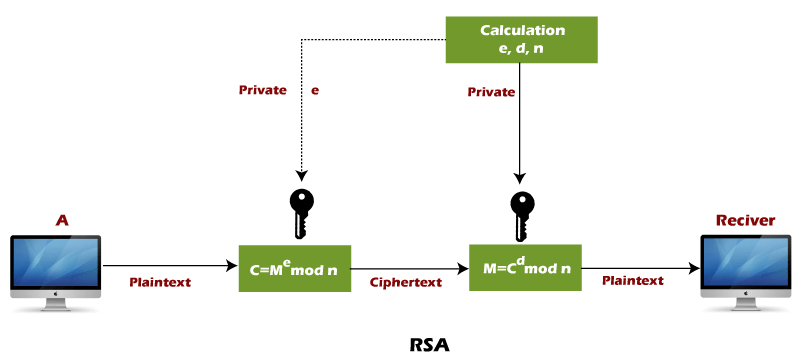
RSA algorithm uses the following procedure to generate public and private keys:

• Pick two large primes  p, q
• Compute  n= p * q and  Φ(n)= (P-1) (Q-1)
• Choose a public key e such that  1<e<Φ(n) gcd(e,Φ(n))=1
• Calculate d such that d= (1+k * Φ(n))/e
• Let the message key be M
• Encrypt: M^e mod N
• Decrypt: C^d mod Nm≡cdmodn

Exercise – I

P and Q are two prime numbers. P=7 and Q=17. Take public key E=5. 

If plain text value is 6. Then what will be cipher text value according to RSA algorithm? 

Again calculate plain text Value from cipher text.

Solution:

 Here P=7, Q=17, E=5, M=6, n=?, Φ(n)=?, D=? and C=?

Modulus of N is:

N= P * Q

   = 7 * 17

 N= 119

Calculate Euler’s Totient Phi Value:

Φ(n)= (P-1) (Q-1)

         = (7-1) (17-1)

         = 6 * 16

 Φ(n)= 96

Calculate Private Key D Value:

Formula: 

D= (1+K. Φ(n))/E Here K is 0,1,2,3,……

   = (1+4 * 96)/5 Here K=4

   = 385/5

 D= 77

Calculate Cipher text(Encryption):

C = M^E Mod N

   = 6⁵ Mod 119

   = 7776 Mod 119

   = 41

According to RSA algorithm, the Cipher Text is 41.

Calculate Plain text(Decryption):

M = C^D Mod N

     = 41⁷⁷ Mod 119

     = ((41¹⁰ Mod 119) (41¹⁰ Mod 119) (41¹⁰ Mod 119) (41¹⁰ Mod 119)

         (41¹⁰ Mod 119) (41¹⁰ Mod 119) (41¹⁰ Mod 119) (41⁷ Mod 119)) 

         Mod 119

     = (36 * 36 * 36 * 36 * 36 * 36 * 36 * 97) Mod 119

     = 6

As per the RSA algorithm Plaintext from Ciphertext is: 6

Exercise – II

In a public key cryptosystem using RSA algorithm user uses two prime numbers 5 and 7. 

He chooses 11 as Encryption key, find out decryption key. What will be the cipher text, 

if the plain text 2? Decrypt the cipher text. What will be the value of plain text?

Solution:

 Here P=5, Q=7, E=11, M=2, N=?, Φ(n)=?, D=? and C=?

Modulus of N is:

N= P * Q

   = 5 * 7

 N= 35

Calculate Euler’s Totient Phi Value:

Φ(n)= (P-1) (Q-1)

         = (5-1) (7-1)

         = 4 * 6

 Φ(n)= 24

Calculate Private Key D Value:

Formula: 

D= (1+K. Φ(n))/E       Here K is 0,1,2,3,……

   = (1+5 * 24)/11        Here K=5

   = 121/11

 D= 11

Calculate Cipher text(Encryption):

C = M^E  Mod N

   = 2¹¹ Mod 35

   = 2048 Mod 35

   = 18

According to RSA algorithm, the Cipher Text is 18.

Calculate Plain text(Decryption):

M = C^D Mod N

     = 18¹¹ Mod 35

     = ((18⁵ Mod 35) (18⁶ Mod 35) Mod 35

     = (23 * 29) Mod 35

     = 667 / 35

     = 2

As per the RSA algorithm Plain text from Cipher text is: 2

Exercise – III

P and Q are two prime numbers. P=17 and Q=11. Take public key E=7. 

If plain text value is 5. Then what will be cipher text value and private key value according to RSA algorithm? 

Again calculate plain text value from cipher text.

Solution:

 Here P=17, Q=11, E=7, M=5, N=?, Φ(n)=?, D=? and C=?

Modulus of N is:

N= P * Q

   = 17 * 11

 N= 187

Calculate Euler’s Totient Phi Value:

Φ(n)= (P-1) (Q-1)

         = (17-1) (11-1)

         = 16 * 10

 Φ(n)= 160

Calculate Private Key D Value:

Formula: 

D= (1+K. Φ(n))/E       Here K is 0,1,2,3,……

   = (1+1 * 160)/7        Here K=1

   = 161/7

 D= 23

Calculate Cipher text(Encryption):

C = M^E  Mod N

   = 5⁷ Mod 187

  = 78125 Mod 187

   = 146

According to RSA algorithm, the Cipher Text is 146.

Calculate Plain text(Decryption):

M = C^D Mod N

     = 146²³ Mod 187

     = ((146³ Mod 187) (146³ Mod 187) (146³ Mod 187) 

          (146³ Mod 187) (146³ Mod 187) (146³ Mod 187) 

          (146³ Mod 187) (146² Mod 187))Mod 187

     = (((82 * 82 * 82) Mod 187) ((82 * 82 * 82) Mod 187) 

        ((82 * 185) Mod 187)) Mod 187

     = (92 * 92 * 23) Mod 187

     = 194672 / 187

     = 5

As per the RSA algorithm Plain text from Cipher text is: 5

Exercise – IV

P and Q are two prime numbers. P=3 and Q=11. Take public key E=3. 

f original message is 00011011. Then what will be cipher text value and private key value according to RSA algorithm? 

Again calculate plain text value from cipher text.

Solution:

 Here P=3, Q=11, E=3, M=00011011, N=?, Φ(n)=?, D=? and C=?

Modulus of N is:

N= P * Q

   = 3 * 11

 N= 33

Calculate Euler’s Totient Phi Value:

Φ(n)= (P-1) (Q-1)

         = (3-1) (11-1)

         = 2 * 10

 Φ(n)= 20

Calculate Private Key D Value:

Formula: 

D= (1+K. Φ(n))/E       Here K is 0,1,2,3,……

   = (1+1 * 20)/3        Here K=1

   = 21/3

 D= 7

The Message is given in binary number format that has to be converting into decimal number:

= 0 * 2⁷ + 0 * 2⁶ + 0 * 2⁵ + 1 * 2⁴ + 1 * 2³ + 0 * 2² + 1 * 2¹ + 1 * 2⁰ 

= 0 * 128 + 0 * 64 + 0 * 32 + 1 * 16 + 1 * 8 + 0 * 4 + 1 * 2 + 1 *1

= 0 + 0 + 0 + 16 + 8 + 0 + 2 + 1

= 27

Calculate Cipher text(Encryption):

C = M^E  Mod N

   = 27³ Mod 33

  = 19683 Mod 33

   = 15

According to RSA algorithm, the Cipher Text is 15.

Calculate Plain text(Decryption):

M = CD Mod N

     = 15⁷ Mod 33

     = ((15³ Mod 33) (15⁴ Mod 33)) Mod 33

     = (9 * 3) Mod 33

     = 27 / 33

     = 27

As per the RSA algorithm Plain text from Cipher text is: 27 : 00011011

Exercise – V

P and Q are two prime numbers. P=13 and Q=17. Take public key E=19. 

If original message is 12. Then what will be cipher text value and private key value according to RSA algorithm? 

Again calculate plain text value from cipher text.

Solution:

 Here P=13, Q=17, E=19, M=12, N=?, Φ(n)=?, D=? and C=?

Modulus of N is:

N= P * Q

   = 13 * 17

 N= 221

Calculate Euler’s Totient Phi Value:

Φ(n)= (P-1) (Q-1)

         = (13-1) (17-1)

         = 12 * 16

 Φ(n)= 192

Calculate Private Key D Value:

Formula: 

D= (1+K. Φ(n))/E       Here K is 0,1,2,3,……

   = (1+9 * 192)/19        Here K=9

   = 1729/19

 D= 91

Calculate Cipher text(Encryption):

C = M^E  Mod N

   = 12¹⁹ Mod 221

  = 181

According to RSA algorithm, the Cipher Text is 181.

Calculate Plain text(Decryption):

M = C^D Mod N

     = 181⁹¹ Mod 221

     = 12

As per the RSA algorithm Plain text from Cipher text is: 12.